Aspect ratio is important in defining the flow rate through a hole, but hole diameter and the agitation speed are equally significant.

Download a PDF containing all equations, figures and tables for this article

It has been the conventional wisdom of the industry that the predominant board parameter associated with through-hole plating is the aspect ratio. While this is intuitively understandable, very little has been done to analytically verify the assertion. This paper will explore this hypothesis by developing a first principle flow model using the Navier-Stokes analog for viscous fluids. The first concern is to define the proper flow regime – laminar or turbulent – based on the Reynolds Number associated with the process. Once this is established, a proper mathematical model can then be identified. At that point, the governing equations are parameterized and the crucial parameters identified. Faraday’s Law will then be folded into the model to define an algebraic model for electrolytic plating. Finally, an order of magnitude analysis is presented to determine the relative importance of the critical parameters.

Introduction

The theory of through-hole plating has evolved primarily from anecdotal and empirical evidence as well as hearsay. Very little has been forthcoming to present a defendable mathematical analysis of the process. Doing so will require combining the physics of fluid mechanics and electrochemistry. The importance of such an analog is to both identify the parameters that govern the process, as well as the degree to which a particular variable impacts the process. For instance, it is well accepted that the aspect ratio of the through hole plays an important role in the process, but it is not understood if the impact is linear, sub-linear or super linear. This analysis will provide that insight.

First, the flow regime – turbulent or laminar – will be determined followed by development of the governing equations describing the fluid mechanics of the plating process. This will then be coupled with the governing laws of electroplating (Faraday’s second law) to complete the analog.

Flow Regime

The flow regime is determined by the dimensionless Reynolds Number. For the case at hand, a good and well-developed analogy is the flow in a linear pipe. This type of flow is referred to as Hagen-Poiseuille Flow, and the Reynolds Number is given by:

[Equation 1]

Where and for our purposes:
u₀ is the mean velocity of the fluid in the hole (we will use 10 ft./min. to maximize the Reynolds Number)
d is the diameter (we will use 30 mils to again maximize the Reynolds Number)
v is the kinematic viscosity (for most acids 0.00016 ft.2/sec.)

The numerical value of the Reynolds Number in this case is: R=2.6

It is generally accepted that the flow will be laminar, as opposed to turbulent, for a Reynolds Number less than 2300. Keep in mind that the Reynolds Number is a point function, and the flow can vary between laminar and turbulent over a very small distance.

The Governing Equations of Fluid Mechanics

In this case, as depicted in Figure 1, plating fluid passes through a through hole and is governed by equations known as the Navier-Stokes equations. When adapted to the case at hand, the result¹ is expressed as seen in the following equation:

[Equation 2]

r is the radius of the hole and y the radial distance from the center of the hole to some position in the flow.

The mean velocity (u₀), which will become of great importance in the next section on electroplating, is

[Equation 3]

where µ is the viscosity

and

[Equation 4]

V is the speed of the plating fluid relative to the surface being plated and ρ the density. The numerator is often referred to as the dynamic pressure and is the pressure component associated with a moving fluid.

The volume flow rate is:

[Equations 5 and 6]

where A is the aspect ratio of the hole.

It is desirable to maximize the volume flow rate. Conventional wisdom has been that the volume flow rate is inversely proportional to the aspect ratio, which is in agreement with the analysis. Even more important is the hole diameter, which has a super linear impact on the volume flow rate and explains why small holes are difficult to plate even at relatively low aspect ratios. It is also seen that the relative velocity or agitation speed also plays a super linear role. These effects are shown in Figures 2 and 3.

In summary, while the aspect ratio is a very important parameter in defining the flow rate in a hole, both the hole diameter and the agitation speed are even more significant.

Electroplating Issues

The next step in this analysis is to combine the laws of electrochemistry into the above analysis. The physics of electroplating were first developed by Faraday. According to Faraday’s Law, the number of moles of material plated at a cathode is proportional to the number of moles of electrons transferred at that electrode² or:

w = GIt

The rate of deposition is then:

Where w is the amount of material plated, G is a constant, I is the effective current and t is time.

The effective current is primarily a function of the concentration of the plating solution. Normally, the concentration of the bulk bath is very near the maximum level, and the plating process is said to be 100% efficient, but as the concentration, decreases the effective current becomes³:

Where:
I₀ is the total current supplied to the plating bath
k is a constant (plating bath efficiency)
c is the local concentration
c₀ is the maximum concentration (concentration of the bath at large)

Since the plating bath is usually very large compared to the cathode, the bulk concentration of the bath will be assumed to be constant at c₀. The concentration of the plating solution in the through hole, however, decreases as the plating fluid transverses the hole. The analysis requires an algebraic expression for this mechanism.

Plated Through-Hole Dynamics

In Figure 4, a control volume of plating fluid is shown moving through the PTH at a speed of u and plating the surface of the barrel at a local rate

To an observer attached to the control volume, the rate of change of the concentration in the control volume

is:

[Equation 9]

where V is volume of the control volume.

Combining Equations 7, 8 and 9 and then integrating using the identity that c=c₀ at x=0, the result is a relationship between the concentration and the position in the barrel.

[Equation 10]

where

is the plating rate at the surface of the cathode.

The velocity (u) of the control volume is given by Equation 3.

Also it is pointed out in the National Metals Finishing Resource Bluebook that the plating efficiency of a copper bath is approximately 10% when the concentration is 2.86 g/ft³. In that case, the value of k is:

The plating bath index, which can be influenced by plating bath additives such as “levelers,” is defined as:

In this case X = 0.0367
k = 0.0367c₀

The relationship between the position in the barrel (x/l) and the concentration becomes:

[Equation 11]

Equation 11 defines the concentration along the barrel of the PTH; unfortunately, however, the relationship is implicit. That is, one cannot solve directly for the concentration and, consequently, a numerical technique is needed.

With the concentration defined, the plating efficient follows (see Equation 8). Then using Faraday’s Law (Equation 7), it is now possible to calculate the theoretical plating thickness anywhere in the barrel. It will be noticed in Equation 11 the controlling parameters are:

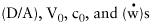
It has long been empirically realized that plating becomes more difficult with increasing hole aspect ratio, but Equation 11 shows that the hole diameter plays an equally important role separate and apart from the aspect ratio. It is also common knowledge that through-hole plating is improved with agitation. Equation 11, in fact, finds the agitation speed plays a super linear role. The concentration of the bath is also important, as is the plating rate at the surface. The surface-plating rate is principally a function of the applied current I0, which demonstrates that low amperage plating will improve the uniformity of PTH side wall, which has recently been the observation of several leading-edge PCB shops. The plating profiles are demonstrated as a function of these variables. This will be accomplished by using variations from the Based Line Parameters shown in the Table 1.

The first variation shown in Figure 5 looks at the effect of aspect ratio and hole diameter. As the aspect ratio is increased, the plating thickness along the hole-wall is reduced in a nonlinear manner. It is also noticed that as the hole diameter decreases, the plating thickness quickly subsides causing a substantial nonlinear variation in the thickness of copper along the barrel. For instance, at an aspect ratio of 6, the impact of the hole diameter is minor, but at an aspect ratio of 14, the impact is severe.

This information is now summarized by viewing the minimal through-hole plating thickness, which occurs halfway through the barrel after being normalized to the surface plating rate. A value of 1.0 is the desirable result.

The effect of the hole diameter at the 50% barrel position is shown in Figure 6 followed by a similar graph for the aspect ratio as shown in Figure 7.

The predicted effect of the other parameters on the minimal plating thickness is shown in Figures 8, 9, 10 and 11.

Summary

The analysis concludes that the conventional wisdom concerning the variables that drive an electroplating through-hole process is correct but incomplete. This analysis finds that, in addition to the aspect ratio, there are several other variables of equal importance that should also be considered. These variables and the magnitude of their impact on plating are listed in Table 2. PCD&F

Ed note: This article was originally presented at the IPC Expo conference, February 2007 in Los Angeles, CA.

Dr. Lee Parker is president of JLP Consultants LLC. He can be reached at This email address is being protected from spambots. You need JavaScript enabled to view it..

References
1. Schlichting, Herman, Boundary Layer Theory, McGraw Hill Book Company.
2. Faraday’s Law, The Columbia Encyclopedia, Sixth Edition.
3. National Metals Finishing Resource, Bluebook, Pollution Prevention and Control Technologies for Plating Operations.

• Prev
• Next