Printed Circuit Design & Fab Online Magazine - Modeling Common Ground Noise in High-Speed Multi-board PCB Systems

The amount of noise between reference planes in two adjoining boards depends on the inductance produced by the inter-board connector.

The high-speed link paths in today’s computer systems frequently span across multiple circuit boards. These signal paths on multiple boards are connected through connectors and cables, which often introduce impedance discontinuities. The challenges presented by multi-board signaling have been addressed in most high-speed interfaces by using differential signaling, which is less severely impacted by connector discontinuities. However, one pitfall of differential signaling is the tendency to ignore the accompanying common mode signal and mode conversion effects. Signal integrity tools often consider only the differential-to-differential parameters (SDD11 and SDD21), ignore other mixed mode S-parameters, and assume that the reference planes in each circuit board are tied perfectly to a common ground. Therefore, this kind of methodology fails to capture the common mode effects on signals. The true scenario, however, is that at high frequencies the reference planes in multi-board systems are independent, and therefore significant noise voltages can develop between reference planes due to common mode currents flowing through the connectors. This noise voltage is a function of the common mode current and the loop inductance of the connector as seen by the signal line. In this paper, the impact of the non-ideal common ground on the electrical behavior of multi-board differential signaling is studied. In particular, the amount of common mode signal present in a realistic design, the amount of inductance created by a signal line due to inter-board connectors, the amount of noise between reference planes in two adjoining boards, and the overall impact on the high speed differential signals are described.

Common Mode Signal Due to Non-Ideal Common Ground

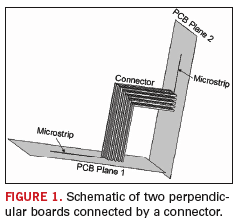
In a multi-board system, signals are transmitted throughout the boards using either microstrip or stripline transmission lines. FIGURE 1 shows an example of an interface where two boards with microstrip lines are connected through connector pins, bent at an angle that properly connects one plane to the other. Some of the pins in the connector are designated as the ground pins that connect to the ground planes. The actual configuration of the ground pins will impact inductance (as discussed in a later section) and is therefore important for the performance of the design. In this section, the existence of common mode noise due to non-ideal common ground connection for the example shown in Figure 1 is demonstrated.

Fig. 1

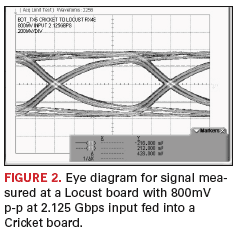
Measurement data proves the importance of considering non-ideal common ground for realistic signal integrity analysis. FIGURE 2 shows an eye diagram measurement obtained from a parallel bit error rate tester (parBERT) when a 800 mV p-p differential signal is transmitted through the device under test (DUT) at 2.125 Gbps using a PRBS7 bit pattern. The DUT includes a driver test card attached to a back plane through an AIRMAX connector, with a receiver test card attached through a GBX connector. SMA cables from the parBERT generator are attached to the driver test card SMA connectors. The SMA connectors on the receiver test card feed into a sampling scope for capturing the eye waveform. It can be seen from Figure 2 that the eye height is approximately 440 mV. 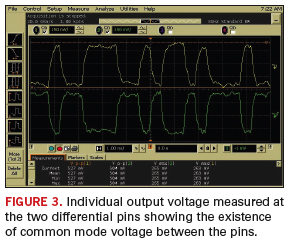The measured voltage waveforms, relative to ground, on individual pins of the differential pair at the receiver side are shown in FIGURE 3. Differential receivers effectively subtract these two signals to get the final waveform. It can be noted that the sum of the two voltages are not zero, which indicates the presence of common mode voltage. 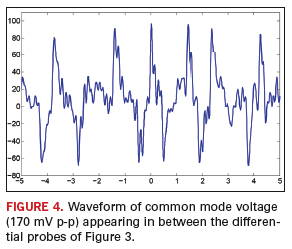This common mode voltage appearing between the pins of the differential pair at the receiver side is plotted in FIGURE 4. It can be seen that the peak-to-peak magnitude of the common mode voltage is around 170 mV, which will greatly affect the signal integrity of the multi-board system by generating ground-to-ground noise. 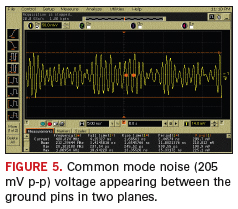FIGURE 5 shows the common mode noise appearing between the ground pins of the AIRMAX connector on the driver test card and the back plane. The magnitude of the common mode noise is about 205 mV for the 2.125 Gbps input. This ground-to-ground noise will severely affect the signal integrity of the design and cannot be captured using conventional signal integrity analysis, as discussed in a later section. Therefore, it can be concluded that the impedance discontinuity at the board interfaces, which is conventionally ignored, must be considered for realistic signal integrity analysis.

Fig. 2

Modeling of PCB Connectors for Inductance Extraction

The common mode noise that appears between the ground pins in different boards will depend on the common mode current and the loop inductance of the signal lines at the connector. Therefore, accurate analysis and successful design of PCBs with multiple boards connected to a main board need to factor in the loop inductance contributed by the connectors, which depends on the actual current return paths. Since the common mode current flowing through the signal pin returns through the ground pins, the separation of the signal pin from the ground pins and their relative positioning plays an important role in determining the loop inductance. Finding the pin configuration that minimizes inductance is very important for PCB signal integrity. In this paper, Partial Element Equivalent Circuit (PEEC) method, and magnetic energy conservation method are employed to efficiently analyze inductance.

The PEEC Model. The model of Figure 1 is implemented in IBM’s PEEC solver, PowerPEEC. Small lengths of microstrip lines with a characteristic impedance of 50 Ω are used to obtain the inductance as seen by the microstrip lines. The actual dimensions of the AIRMAX connector’s pins are used for modeling the DUT. Different possible configurations of the ground pins are considered for estimating the inductance seen at the microstrip line. Depending on the number of grounded pins and their locations, different inductance values are obtained. FIGURE 6 shows four possible configurations and the corresponding inductance values as determined by PowerPEEC. The horizontal spacing of the pins is 2 mm and vertical spacing is 1.4 mm. Note that the white pins are considered as floating for the purpose of inductance computation. The values of inductance show strong dependence on the ground pin configuration, ranging between 16 nH to 37 nH for all the experiments performed on this connector.

Fig. 6

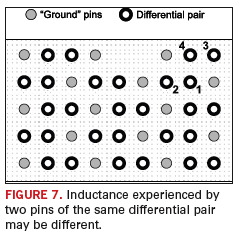
FIGURE 7 illustrates another important point; that the loop inductance seen at two pins of a differential pair may vary depending on their locations. For the AIRMAX connector used in the measurements, the loop inductance for pin 1 is 26.6 nH whereas pin 2 shows 23.6 nH. Similarly, pins 3 and 4 have loop inductances of 31.8 nH and 28.8 nH, respectively. This will cause propagation delay mismatch between the two leads of a differential pair, creating more skew in the connector.

Fig. 7

Although the results obtained by PEEC simulation will be highly accurate, depending on the number of pins, the model size and corresponding simulation time could be large. For example, for the AIRMAX connector, the number of pins could be as high as 120, and the PEEC simulation could take tens of minutes for a single ground pin configuration, making for a time consuming search for the optimal configuration. Therefore, a faster method of exploring different connectors and ground configurations that also yields reasonable accuracy should be used.

Magnetic Energy Conservation Method. For measuring the loop inductance caused by a connector, the method described by Krauter and Mehrotra is found to be appropriate and convenient. The method determines the equivalent loop inductance based upon the conservation of magnetic energy stored in the conductor system. For the AIRMAX connector, each pin has two segments of unequal length – one horizontal and one vertical. For the purpose of inductance computation, a unit current source is applied between the horizontal terminal of the signal pin and the terminal, shorting all horizontal terminals of the ground pins. The terminals of the vertical portion of all pins will be considered shorted assuming quasi-static mode.

For applying the energy-equivalence method to a system consisting of a signal line and N ground lines, let the signal line be represented by the subscript s and the ground lines using gi where i is the index of the ground line. The quantities corresponding to the horizontal (vertical) conductors will be denoted by superscript H (V). Let I be the vector of currents flowing through each pin (with directions signified by the sign of the current value) for unit current through the signal pin. The partial inductance matrices for the horizontal conductors, MH, and the vertical conductors, MV, will be given by the following matrix considering the respective parts only:

Fig. 8

The L terms represent the partial self inductances and the M terms the partial If the equivalent loop inductance is Lloop, which is the total magnetic energy stored for unit signal pin current, then

Fig. 9

This formulation produces a huge speedup in inductance computation – more than four orders of magnitude – with inductance values within 5% of the values obtained from PowerPEEC, as shown in Table 1. Therefore, this formulation can be utilized for determining the optimal ground pin configuration, quick inductance computation for signal integrity analysis and many other applications.

Effects on Eye Diagram

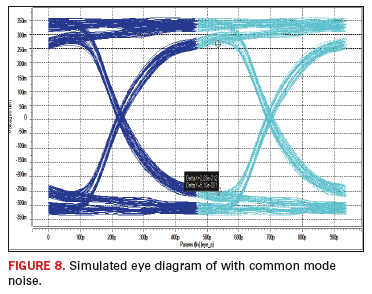
The DUT that produced Figure 2 through Figure 5 is modeled for signal integrity analysis to account for the common mode noise, which is typically ignored in conventional signal integrity simulations. For our simulations, the ground-to-ground noise is injected as a sine wave for simplicity, with peak-to-peak voltage equal to the peak-to-peak ground noise. FIGURE 8 shows the simulated eye diagram, which mimics the parBERT measurement in Figure 2, using 128 random bits simulated in a repeated fashion for 150 ns at 2.125 Gbps. The corresponding eye height is 450 mV, which is slightly more than the value obtained by the parBERT measurement. 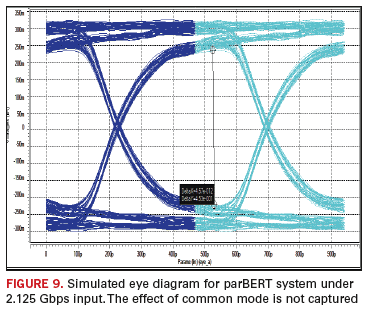It should be mentioned that the effects of two 30-inch SMA cables, two 6.5-inch SMP cables and SMA connector impedance mismatch have been ignored in the simulations. On the other hand, if the ground-to-ground noise is ignored in the signal integrity analysis, the eye diagram of FIGURE 9 with eye height of 510 mV is produced, which is 13% more than the actual value. Therefore, a conventional signal integrity analysis is unrealistic and produces optimistic results.

Conclusions

The effect of non-uniform common mode current return path on common mode noise in high speed differential signals is demonstrated in multi-board systems using both measured and simulated data. There are two points to be noted. First, because of non-ideal common ground connection, significant ground-to-ground noise appears between boards and affects signal integrity in multi-board systems. Signal integrity tools conventionally ignore this effect, which must be factored in for realistic analysis and design of such systems. Second, the amount of noise between reference planes in two adjoining boards depends on the inductance produced by the inter-board connector. Careful choice of the ground pin configuration can help mitigate the effect of common mode noise. PCD&F

Mosin Mondal is a research assistant, ACE Lab, Bruce Archambeault is distinguished engineer, Pravin Patel is senior engineer and technical leader, Samuel Connor is senior engineer, Bhyrav Mutnury is circuit design engineer and Moises Cases is senior member of technical staff, all with IBM. Archambeault can be reached at This email address is being protected from spambots. You need JavaScript enabled to view it..

REFERENCES

1. M. Beattie and L. Pileggi, “Inductance 101: Modeling and Extraction,” in Proc. Design Automation Conference, pp. 323–328, 2001.
2. A. E. Ruehli, “Equivalent Circuit Models for Three Dimensional Multiconductor Systems,” IEEE Transactions on MTT, vol. 22, pp. 216–221, Mar. 1974.
3. B. Krauter and S. Mehrotra, “Layout Based Frequency Dependent Inductance and Resistance Extraction for On-Chip Interconnect Timing Analysis,” in Proc. Design Automation Conference, pp. 303–308, 1998.
4. A. E. Ruehli, “Inductance Calculations in a Complex Integrated Circuit Environment,” IBM Journal of Research and Development, vol. 16, no, 5, pp. 470–481, 1972.