Do corners cause reflections? The answers to last month's puzzle may surprise you.
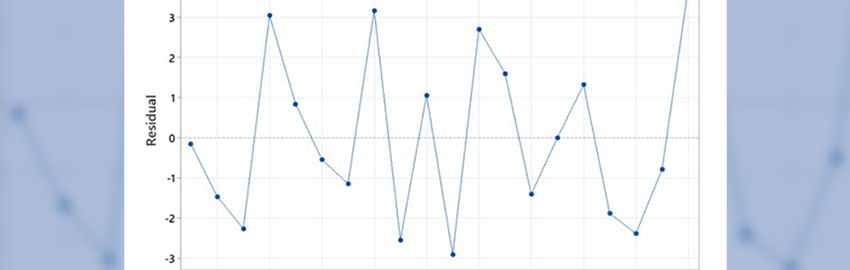
In my January column, I offered a puzzle. In the measured TDR response from a seven-segment, closely coupled 50 Ω serpentine microstrip, it looks like we see the reflections from the six pairs of corners. Figure 1 shows the serpentine and Figure 2 the measured TDR response.
But, is this measured TDR response really an example of reflections from corners? I asked for possible alternative explanations from you, and I had more than 30 e-mail responses.
Half of you wrote, "I always knew corners could cause reflections and now you've demonstrated it." The other half wrote, "I've always heard corners don't cause reflections - it's a myth, so something else is going on."

FIGURE 1. A 50 Ω serpentine microstrip, with each of the seven legs measuring 3" in length.

FIGURE 2. Measured TDR and TDT response from serpentine.
|
First, let me make it perfectly clear:
- Corners can, absolutely, cause reflections.
- The TDR response from this serpentine has nothing at all to do with the corners.
To a signal, a corner represents a small amount of extra capacitance that would not be there if the line width of the signal were constant. It amounts to roughly half a square of metal. In my book, Signal Integrity - Simplified, I show a simple way of estimating the excess capacitance in a corner.
For FR-4 and a 50 Ω line, a corner has about 1.6 x w (line width in inches) pF. If the line width were 0.06", the excess capacitance in a corner would be about 100 fF. This is easily measurable with the right test set up.
Figure 3 shows the measured TDR response of a 50 Ω microstrip test line, 0.06" wide, with four corners. Using the excess capacitance feature of the Agilent DCA86100C with TDR plug-in, we can read the excess capacitance associated with one of the dips from one corner, 96 fF, pretty close to our estimate.

FIGURE 3. Measured TDR response from four corners in the BeTheSignal Master Class workshop demo board.
|
Do corners cause reflections? You bet. Will they cause problems? It depends. If your line width is 0.005" wide, the capacitance in a corner will be about 8 fF. Put this in your simulator and see if it has an impact.
What about the serpentine example above? How would we know if the dips in the TDR trace are due to corners or something else? How do we separate myth from reality? The process we use is "put in the numbers," which we can do by measurement or by calculation.
Let's estimate the impact one of these corners would have in the TDR response. The line width of the serpentine is .015". The capacitance of the corner would be roughly 1.6 x .015 pF = 24 fF. The two corners adjacent to each other would have a capacitance of about 50 fF. As we can see in the TDR response in Figure 3, a 100 fF capacitor gives a reflected signal of about 7 mV out of 200 mV. A 50 fF capacitor would have a reflected signal, with this rise time, of about 3.5 mV.
In the measured TDR response from the serpentine, the first dip has a magnitude of 40 mV. This is an order of magnitude larger than what is expected for a corner. The reflections from the corners cannot explain the dips we see. What else could it be?
A number of you suggested the possibility of far-end noise in the adjacent quiet line as a possible explanation. You are absolutely correct. As the signal travels down leg 1, to the right, forward-going noise is generated in the adjacent leg, also going to the right. At the bend, it loops around to head back to the source, while the signal loops around to go down leg 2. Each time the signal turns a bend, another amount of forward noise heads back to the source and is picked up as a small negative voltage.
This model predicts the six dips. The decrease in amplitude with each bend is due to the increase in the rise time of the signal due to the losses in the line. How can we confirm these dips are due to far-end noise and not to corners? One way is to try a simulation.

FIGURE 4. Agilent ADS equivalent circuit of the serpentine and the simulated TDR and TDT response.
|
In Figure 4, this serpentine trace is simulated with Agilent's ADS circuit simulator. The cross-section geometry of the serpentine is input to the integrated 2D field solver, and a step generator used to emulate a TDR. There are no model elements associated with any corners - it is all about the simulated far-end noise due to coupling between the legs of the serpentine.
The simulated performance of the model closely matches what is observed in the actual serpentine. Which is more likely, that the corners are producing the dips or far-end crosstalk is producing the dips? The only way to know is to put in the numbers. Now you are empowered to separate myth from reality. PCD&M
Dr. Eric Bogatin (This email address is being protected from spambots. You need JavaScript enabled to view it.) is the CTO at IDI, and president of Bogatin Enterprises.