Printed Circuit Design & Fab Online Magazine - Software Simulation Tools for EMC Control of High-Speed Signals

Using multiple simulation techniques and tools improves modeling validity.

The recent explosion of many high-speed nets on PCBs has created a significant challenge for the design engineer to meet the requirements of the commercial standards as well as the specialized requirements for industries like medical, automotive and portable devices.

Simple shielding with metal enclosures is not sufficient to meet the emissions and immunity levels from both regulatory limits as well as industry specific or company specific immunity levels. Typical air flow requirements for cooling high-speed electronics require significant open space in the fan or blower areas of the metal enclosure, effectively limiting the amount of shielding the enclosure can provide. Therefore a combination of good PCB EMC design practice along with shielding must work together to create an effective product solution to the EMC emissions and immunity problems.

There are a number of different levels of software tools available to assist the PCB designer in meeting the EMC requirements. At the most complex level is the fullwave computational electromagnetic solvers, while at the least complex level is the PCB design rule checkers. Both levels of tools can play a significant role in meeting the EMC emissions and immunity requirements with the first design cycle.

A wide range of automated EMI/EMC tools is available to the engineer. These automated tools include design rule checkers that check PCB layout against a set of pre-determined design rules. In addition there are quasi-static simulators, which are useful for inductance/capacitance/resistance parameter extraction when the component is much smaller than a wavelength, and quick calculators using closed-form equations calculated by computer for simple applications. There are fullwave numerical simulation techniques that will give a very accurate simulation for a limited size problem and expert-system tools, which provide design advice based on a limited and predetermined set of conditions. It is clear that these different automated tools are applied to different EMI problems, and at different times in the design process.

Automated EMC Design Rule Checking

The EMC performance of a printed circuit board is mostly based on the location of the various components and the location of the various critical high-speed and I/O nets/traces. Manual checking of all the various layers of today’s high-speed circuit boards is too time consuming and prone to human error. Automated rule checking software relieves the tedium, and removes the human error by reading the CAD design file, taking each critical net/trace in turn, and checking that it does not violate any of the most important EMC design rules.

The usefulness of this kind of tool is largely based on EMC design rules and whatever limits are used for each of the various design rules. Naturally, for different types of industries, some of the design rules will vary, so it is important that the automated design rule checking software allows creation of customer or industry specific rules.

There are many EMC design rules available from many sources. Many of these EMC design rules are in conflict with one another. Therefore, a user might reasonably ask, “Which rule is right for my products?”

Some of the automated EMC design rule checking software implement rules that are based on more detailed laboratory testing and/or fullwave simulations. Each rule should be based on solid electromagnetic physics and not on faith. Users should be very cautious before accepting EMC design rules. These rules should not only have detailed justifications, but should make sense with the basic fundaments of physics. Just because a rule might be commonly accepted does not mean it is right for every product or industry. Remember, it was once commonly accepted that the earth was flat!

Once the appropriate EMC design rules are selected it is time to make sure that all the critical nets/traces and components are selected for checking against the EMC design rules. While computers are fast, typical high-speed PCBs have many hundreds or even thousands of nets/traces, and checking every net/trace can take an excessive amount of time. Critical traces typically include all high-speed signals and signals with very fast rise/fall times. Critical components will be those used for emissions or immunity control, such as decoupling capacitors, filters and electrostatic discharge (ESD) protection devices.

Even with careful PCB layout design, there will typically be many EMC design rule violations. Typical high-speed PCBs have so many constraints (other than EMC), and extremely tight wiring densities that some of the EMC design rules will be violated. It is then up to the design engineer, along with the EMC design engineer, to decide which, if any, of the violations are mild enough to ignore, and which are important enough to justify changing the existing design. An EMC rule violation viewer allows rapid access to the violations by automatically zooming to the violation location, highlighting the trace/net/component that violated the specific rule, and maybe even giving some feedback to the user on the severity of the violation.

Fullwave Electromagnetic Simulation Software

Today’s fullwave EM simulation software tools cannot do everything. That is, they cannot take the complete mechanical and electrical CAD files, compute for some limited time, and provide the engineer with a green/red light for pass/fail for the regulatory standard desired. The EMI and/or design engineer is needed to reduce the overall product into a set of problems that can be realistically modeled. The engineer must decide where the risks are in the product design, and analyze those areas.

Vendor claims must be carefully examined. Vendors might claim to allow an engineer to include detailed PCB CAD designs along with metal shielding enclosures to predict the overall EMI performance. However, these tools are not really capable of such analysis. There are too many things that will influence the final product to make such a prediction with any level of accuracy. On the other hand, these fullwave simulation tools are extremely useful to help the engineer analyze specific parts of the design in order to better understand the physics of the specific feature under study. Then the engineer can use this knowledge to make the correct design decisions and trade-offs.

Tool Box Approach

No single modeling/simulation technique will be the most efficient and accurate for every possible model needed. Unfortunately, most commercial packages specialize in only one technique and try to force every problem into a particular solution. The PCB design engineer and EMI engineer have a wide variety of problems to solve, requiring an equally wide set of tools. The “right tool for the right job” approach applies to EMI engineering as much as it does to building a house or a radio. You would not use a putty knife to cut lumber or a soldering iron to tighten screws, so why use an inappropriate modeling technique?

An extremely brief description of the various fullwave modeling/simulation techniques will be given here. The reader is cautioned that each of these techniques would require a graduate level course to fully understand the details of how they work. The goal of this article is to provide a short overview only, as well as to indicate the strengths and weakness of each technique. Each modeling simulation technique allows the user to solve Maxwell’s electromagnetic equations by using different simplifying assumptions.

Finite-Difference Time-Domain (FDTD)

The FDTD technique is one of the most popular modeling/simulation techniques because of its simplicity. FDTD uses a volume-based solution approach to Maxwell’s differential equations. Maxwell’s equations are converted to central difference equations, and solved directly in the time domain. The entire volume of space surrounding the object to be modeled must be gridded, usually into square or rectangular grids. Each grid must have a size that is small compared to the shortest wavelength of interest (since the simplifying assumption is that the amplitude of the EM fields within a grid will be constant), and have its location identified as metal, air or whatever material desired. The location of the electric and magnetic fields are typically offset by a half grid size. Figure 1 shows an example of such a grid for a two-dimensional case. Once the grid parameters are established, the electric and magnetic fields are determined throughout the grid at a particular time. Time is advanced one time step, and the fields are determined again. Thus, the electric and magnetic fields are determined at each time step based on the previous values of the electric and magnetic fields.

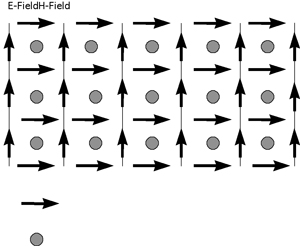
FIGURE 1. Two-dimensional FDTD grid.

Once the fields have propagated throughout the meshed domain, the FDTD simulation is complete and the broadband frequency response of the model is determined by performing a Fourier transform of the time-domain results at the specified monitor points. Since the FDTD method provides a time-domain solution, a wide band frequency-domain result is available from a single simulation.

Because the FDTD technique is a volume-based solution¹, the edges of the grid must be specially controlled to provide the proper radiation response. The edges are modeled with an absorbing boundary condition (ABC). There are a number of different ABCs, mostly named after their inventors. In nearly all cases, the ABC must be electrically remote from the source and all radiation sources of the model, so that the far-field assumption of the ABC holds true, and the ABC is reasonably accurate (usually about 1?6 of a wavelength at the lowest frequency of interest). Typically, a good ABC for the FDTD technique will provide an effective reflection of less than –60 dB.

Naturally, since the size of the gridded computational area is determined from the size of the model itself, some effort is needed to keep the model small. The solution time increases directly as the size of the computational area (number of grid points) increases. The FDTD technique is well suited to models containing enclosed volumes with metal, dielectric and air. As with all volume-based techniques, the dielectrics do not require additional computer memory. The FDTD technique is not well suited to modeling wires or other long, thin structures, as the computational area overhead increases very rapidly with this type of structure. As with all time domain simulation techniques, the simulation must run for enough time steps to completely contain one full cycle for the lowest frequency of interest.

Method of Moments (MoM)

The MoM is a surface current technique². The structure to be modeled is converted into a series of metal plates and wires³. Figure 2 shows an example of a shielded box converted to a wire grid with a long attached wire. Once the structure is defined, the wires are broken into wire segments (short compared to a wavelength since the simplifying assumption is that the current amplitude will not vary across the wire segment) and the plates are divided into patches (small compared to a wavelength). From this structure, a set of linear equations is created. The solution to this set of linear equations finds the RF currents on each wire segment and surface patch. Once the RF current is known for each segment and patch, the electric field at any point in space can be determined by solving for each segment/patch and performing the vector summation.

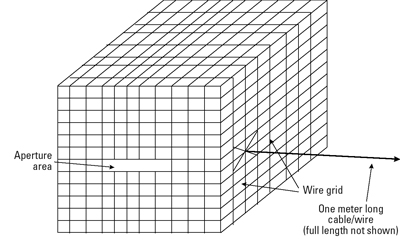
FIGURE 2. MoM wire mesh model of shielded enclosure with long cable attached.

When using the MoM, the currents on all conductors are determined and the remaining space is assumed to be air. This facilitates the efficiency of the MoM in solving problems with long thin structures, such as external wires and cables. Since the MoM finds the currents on the conductors, it models metals and air very efficiently. Dielectric and other materials are difficult to model using the MoM with standard computer codes and require many more unknown currents, creating problems that require much more RAM memory.

The MoM is a frequency-domain solution technique. Therefore, if the solution is needed at more than one frequency, the simulation must be run for each frequency. This is often required, since the source signals within the typical computer have fast rise times, and therefore wide harmonic content.

MoM is very well suited for problems with long wires or large distances, since the air around the object does not increase the amount of RAM memory required, as in the cases for all volume-based techniques. However, MoM is not well suited to shielding effectiveness problems, nor is it well suited to problems with finite sized dielectrics due to the large amount of memory required.

Finite Element Method (FEM)

The FEM is another volume-based solution technique. The solution space is split into electrically small elements, usually triangular or tetrahedral shaped and referred to as the finite element mesh. As in the case of FDTD, the simplifying assumption is that the fields are constant within each mesh element. The field in each element is approximated by low-order polynomials with unknown coefficients. These approximation functions are substituted into a variational expression derived from Maxwell’s equations, and the resulting system of equations is solved to determine the coefficients. Once these coefficients are calculated, the fields are known approximately within each element.

As in the above techniques, the smaller the elements, the more accurate the final solution. As the element size becomes small, the number of unknowns in the problem increases rapidly, increasing the solution time.
The FEM is a volume-based solution technique; therefore, it must have a boundary condition at the boundary of the computational space. Typically, the FEM boundaries must be electrically distant away from the structure being analyzed (typically one full wavelength at the lowest frequency of interest), and must be spherical or cylindrical in shape. This restriction results in a heavy overhead burden for FEM users, since the number of unknowns is increased dramatically in comparison to other computational techniques.

FEM is well suited to problems with large variations in mesh size (within the limitations of remaining electrically small) since the mesh is an unstructured mesh. It is also well suited to problems completely contained within metal boundaries, since the ABC issues are not a limitation. FEM is not well suited to problems with open radiation boundaries because of ABC issues, nor is it well suited to problems with long wires.

Finite Integration Technique (FIT)

Unlike the FDTD method, which uses the differential form of Maxwell’s equations, the FIT discretizes Maxwell’s equations written in their integral form. The unknowns are thus electric voltages and magnetic fluxes rather than field components along the three space directions. Like all full 3D methods, the entire 3D domain must to be meshed with electrically small meshes. For Cartesian grids however, a special technique called perfect boundary approximation (PBA) eliminates the staircase approximation of curved boundaries, for both PEC/dielectric and dielectric/dielectric interfaces. It allows even strongly non-uniform meshes, thus maintaining a manageable computational size. The FIT can be applied in both time domain (as the FDTD), and frequency domain (like FEM), on Cartesian, non-orthogonal-hexahedral or tetrahedral grids. In the time domain, the explicit formulation leads to small memory requirements and allows solving very large problems. From the time domain results, broadband, high-resolution frequency-domain quantities are obtained by Fourier transform. If the FIT is used directly in the frequency domain, the resulting matrices are sparse. The FIT is applicable to a variety of electromagnetic problems: in bounded or unbounded domains, for electrically small or very large structures, in inhomogeneous, lossy, dispersive or anisotropic materials. Its strengths and weaknesses are similar to FDTD, with the additional strengths mentioned above.

Partial Element Equivalent Circuit Model (PEEC)

PEEC is based on the integral equation formulation of Maxwell’s equations and is a surface-based technique like MoM. The electromagnetic coupling between elements is converted to lumped element equivalent circuits with partial inductances, capacitances, resistances and partial mutual inductances. All structures to be modeled are divided into electrically small elements, since the simplifying assumption is that the current is constant in each element. An equivalent circuit describes the coupling between elements and includes propagation delay. Once the matrix of equivalent circuits is developed, then a circuit solver can be used to obtain a response for the system. One of the main advantages in using the PEEC method is the ability to add circuit elements into an EM simulator to model lumped circuit characteristics and to operate at all frequencies, including DC. PEEC’s limitations are similar to MoM.

Transmission Line Method (TLM)

TLM belongs to the general class of differential (volume-based) time-domain numerical modeling methods. It is similar to the FDTD method in terms of its capabilities. Like FDTD, analysis is performed in the time domain and the entire region of the analysis is gridded with electrically small elements. The TLM model is formed by conceptually filling the computational domain with a network of 3D transmission-lines in such a way that the voltage and current give information on the electric and magnetic fields. The point at which the transmission-lines intersect is referred to as a node, and the most commonly used node for 3D work is the symmetrical condensed node. Additional elements, such as transmission-line stubs, can be added to the node so that different material properties can be represented. Instead of interleaving E-field and H-field grids as in FDTD, a single grid is established and its nodes are interconnected by virtual transmission lines. At each time step, voltage pulses are incident upon the node from each of the transmission lines. These pulses are then scattered/reflected to produce a new set of pulses that become incident on adjacent nodes at the next time step.

The strengths of the TLM method are similar to those of the FDTD method. Complex, nonlinear materials are readily modeled. The weaknesses of the FDTD method are also shared by this technique. The primary disadvantage being that problems with long wires require an excessive amount of computer memory.

Quasi-Static Simulation Software

When an object is electrically very small – compared to the wavelength of the highest frequency of interest – then quasi-static simulation tools can be used. The fundamental assumption is that there is no propagation delay between elements within the model.

Quasi-static tools are very useful for creating an equivalent circuit of inductance, capacitance and resistances that can be solved with circuit solvers such as SPICE. Matrices of many elements can be used for including complex PCB connectors in signal integrity simulations.

Other Software Tools

There are a wide variety of software tools available to do specific tasks. The user must carefully consider if the software tool will do the type of analysis that is required. For example, some vendors offer simulation software that will read complete CAD files, and then predict the far field emissions level based on the simple loop formed by a microstrip and the return/ground plane. This simplifying assumption is too simple for most applications, since the far field emissions are most often directly controlled by the metal shield (and the openings) as well as long attached wires, and not directly from the traces on the board. While the traces on the PCB might be the initial case of the emission, the coupling to other features, because of the metal shield and/or cables, is the dominant effect. This dominant effect is ignored by these tools, and can lead to dangerous and disastrous decisions when used incorrectly.

Proper Simulation Validation

In the early years of EM simulation, the practitioners were experts in EM theory and simulation techniques, and often wrote their own programs to perform the simulations. However, modeling and simulation is no longer restricted only to experts. The commercially available codes are diverse, easy to use and provide the user with convenient means to display results. New users can begin using these codes quickly without the requirement of being expert.

The danger that is not highlighted by vendors or creators of simulation software is the need to validate the simulation results. It is not sufficient to simply believe a particular software tool provides the correct answer. Some level of confidence in the results are needed beyond a religious-like trust in a software tool simply because others use it, because the vendor assures their customers of the tool’s accuracy, or because others have validated their results in the past.

There are three different levels of model validation. When deciding how to validate a model, it is important to consider which level of validation is appropriate. The levels are:

n Computational technique validation
n Individual software code implementation validation
n Specific problem validation

Computational Technique Validation

The first level of model validation is the computational technique validation. This is usually unnecessary in most CEM modeling problems, since the computational technique will have been validated in the past by countless others. If a new technique is developed, it too must undergo extensive validation to determine it’s limitations, strengths and accuracy but, if a “standard” technique such as the FDTD, MoM, PEEC, TLM and FEM, etc. is used, the engineer need not repeat the basic technique validation. This is not to say, however, that incorrect results will not occur if an incorrect model is created or if a modeling technique is used incorrectly.

Individual Software Code Implementation Validation

The next level of validation is to ensure the software implementation of the modeling technique is correct, and creates correct results for the defined model. Naturally, everyone who creates software intends it to produce correct results; however, it is usually prudent to test individual codes against the types of problems for which they will be used.

For example, a software vendor will have a number of different examples where their software code has been used, and where tests or calculations have shown correlation with the modeled results. This is good, and helps the potential user to have confidence in that software code for those applications where there is good correlation. However, this does not necessarily mean that the software code can be used for any type of application and still produce correct results. There could be limitations in the basic technique used in this software, or there could be difficulties in the software implementation of that specific problem. When a previous validation effort is to be extended to a current use, the types of problems that have been validated in the past must closely match the important features of the current model.

Specific Problem Validation

Specific model validation is the most common concern for engineers. In nearly all cases, software-modeling tools will provide a very accurate answer to the question that was asked. However, there is no guarantee that the correct question was asked. That is, the user may have inadvertently specified a source or some other model element that does not represent the actual physical structure intended. The most common ways to validate a simulation result is to use either measurements or a second simulation technique.

It is often overlooked that it’s important to duplicate the same problem in both the modeling and the measurement cases. All important features must be included in both. Laboratory measurement limitations must be included in the model. For example, the EMI emissions test environment (OATS vs. anechoic vs. semi-anechoic, etc.), antenna height and the antenna pattern will likely have a significant effect on the measurement, which, if not included in the simulation, will cause the results to differ. One of the advantages of simulation is that a “perfect” environment can be created, allowing the user to focus on the desired effects without consideration of the difficulties of making a measurement of only the effect desired.

Another important consideration is the loading effect of the measurement system on the device under test. For example, when a spectrum analyzer or network analyzer is used to measure effects on a printed circuit board the loading effect of the input impedance for the spectrum/network analyzer (typically 50 Ohms) must be included in a simulation. While the 50-Ohm load of the analyzer does not necessarily represent the real-world environment that the PCB will be operating in, it becomes very important when a simulation is to be compared to a laboratory measurement.

Measurement accuracy and repeatability is another important consideration to model validation by measurement, depending on the application. While most engineers take great comfort in data from measurements, the repeatability of these measurements in a commercial EMI/EMC emissions test laboratory is poor. The differences between measurements taken at different test laboratories, or even within the same test laboratory on different days, can be easily as high as +/- 6 dB. The poor measurement accuracy or repeatability is due to measurement equipment, antenna factors, site-measurement reflection errors and cable movement optimization. Laboratories that use a plain-shielded room test environment are also considered to have a much higher measurement uncertainly. Some CEM applications, such as RCS, have a much more controlled environment, and therefore measurement validation is a good choice.

Model Validation Using Multiple Simulation Techniques

Another popular approach to validating simulation results is to model the same problem using two different modeling techniques. If the physics of the problem are correctly modeled with both simulation techniques, then the results should agree. Achieving agreement from more than one simulation technique for the same problem can add confidence to the validity of the results.

As described above there are a variety of fullwave simulation techniques. Each has strengths and weaknesses. Care must be taken to use the appropriate simulation techniques and to make sure they are different enough from one another to make the comparison valid. Comparing a volume-based simulation technique (FDTD, FEM, FIT, TLM) with a surface-based technique (MoM, PEEC) is preferred because the very nature of the solution approach is very different. While this means that more than one modeling tool is required, the value of having confidence in the simulation results is much higher than the cost of a few vendor software tools.

By the very nature of fullwave simulation tools, structure-based resonances often occur. These resonances are an important consideration to the validity of the simulation results. Most often, the simulations of real-world problems are subdivided into small portions due to memory and model complexity constraints. These small models will have resonant frequencies that are based on their arbitrary size, and have no real relationship to the actual full product. Results based on these resonances are often misleading, since the resonance is not due to the effect under study, but rather it is due to the size of the subdivided model. Care should be taken when evaluating a model’s validity by multiple techniques to make sure that these resonances are not confusing the “real” data. Some techniques, such as FDTD, can simulate infinite planes⁴. Other techniques allow infinite image planes, etc.

There is no one tool that can do everything, and multiple tools, often at different complexity levels, are required. Automated EMI rule checking tools can provide quick and specific analysis of PCB CAD designs, while more complex fullwave simulation tools can provide very accurate and fundamental understanding for limited portions of the overall PCB and/or system. PCD&M

Dr. Bruce Archambeault is an IBM distinguished engineer at IBM in Research Triangle Park, NC. He can be contacted at This email address is being protected from spambots. You need JavaScript enabled to view it..