Why is estimating the effect of a trace on board temperature so complex?
The authors have collaborated over the past 18 months on printed circuit board (PCB) heating and cooling issues.1 They have used a computer simulation modeling tool, TRM,2 in many of their studies. As a result, they have been able to identify the major parameters responsible for trace heating and cooling, and have been able to quantify the effects of many of them. In this article, they will highlight the most important parameters, illustrate their individual effects on trace heating and cooling, and then suggest two areas where additional research is needed.
Traces heat primarily by I2R power dissipation in the trace (FIGURE 1). This part of the dynamic is pretty well understood. The most important variable in this relationship is the resistivity of the conductor material. Traces cool primarily by conduction into the underlying board material, convection into the air, and radiation into space. One of the surprises of IPC-21523 (at least to the PCB design industry) was the dielectric is much more efficient at cooling the trace than is the air or radiation.

Figure 1. The dynamics of trace heating and cooling.
Conduction dynamics are more complicated than they may first appear (FIGURE 2). The typical PCB (dielectric) is made of a resin compound with embedded fiberglass weave that tends to be oriented parallel to the trace. The structure tends to conduct heat better in the horizontal (in-plane) direction than it does the in-vertical (through-plane) direction.
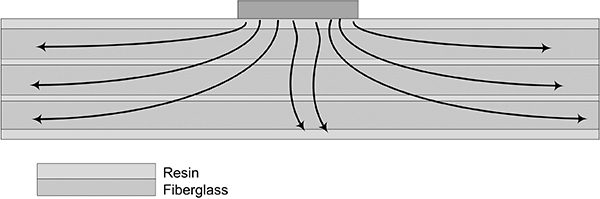
Figure 2. Thermal conduction dynamics.
There is a measure of the board’s ability to conduct heat away from the trace called the “thermal conductivity coefficient.” Board materials are anisotropic, and have different thermal conductivity coefficients for the two directions.4 We will have more to say about this below.
An interesting consequence of this is the cooling path out from under a trace is longer from the centerline of the trace than it is from the edge of the trace (FIGURE 3). Therefore, the edge of a trace cools more efficiently than does the center, and the edge tends to be cooler than the centerline. FIGURE 4 is a thermograph of an actual trace illustrating this phenomenon. This trace is 100 mils wide and 0.5 oz. thick, and carries enough current to heat it to almost 50°C. It can be seen that the trace not only is cooler along the edge than it is along the centerline, but it also does not heat uniformly along the centerline.5

Figure 3. The cooling path is longer from the center of the trace than from the edge of the trace.

Figure 4. Thermograph of 100 mils wide, 0.5 oz. trace heated to around 60°C.
The parameter most associated with the ability of radiation and convection to cool a trace is called the heat transfer coefficient, or HTC. The typical measure of HTC incorporates both the radiation and convection effects into one coefficient, although attempts can be made to separate their effects. The latest version of TRM has an internal calculator for that purpose (FIGURE 5).

Figure 5. Heat transfer coefficient calculator within TRM.
The radiation component of the HTC is reasonably well understood. It is related to Boltzmann’s constant. The convection component is also reasonably well comprehended for a flat plate, but not so much for a small, concentrated hot spot on an otherwise flat plate, which is more typical of a PCB trace. This is one area where more research is needed.
Basic Model for Analysis
To look at the effects the various parameters have on trace heating and cooling, we will develop a standard computer model to start with. That model is a 100 mils-wide, 1.0 oz. thick, 6" long trace on a dielectric (board) measuring 6.5" long by 2" wide. This dielectric is 63 mils thick, which is typical for modern PCBs. It will carry 7A. The following parameters will be used in the base model. They have been found by the authors in previous studies to be typical and reliable.
- Resistivity: 1.68µΩ-cm
- HTC: 11
- Thermal conductivity coefficient:
In-plane 0.6
Through plane 0.4
FIGURE 6 illustrates a thermograph of the results from this basic board. The ambient temperature (initial condition) is 20°C. The hottest spot on the board, the center of the trace, is 56.7°C.
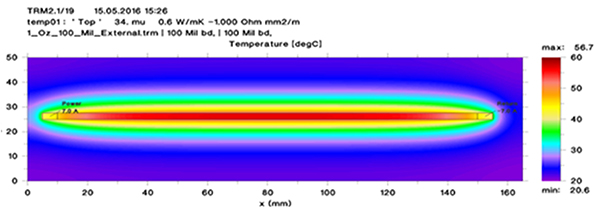
Figure 6. Thermograph of basic model result.
Results of the Analysis
Time to stable temperature. When current is first applied to a trace, there is a time-constant associated with the heating process. That time constant can be found through simulation, but it is difficult to calculate for any given set of conditions. FIGURE 7 is a graph of temperature against time for the basic model. As can be seen, it takes several minutes (four to five) for the temperature to rise close to its maximum value. For higher currents and hotter temperatures, it can take from six to 10 minutes for the temperature to stabilize.
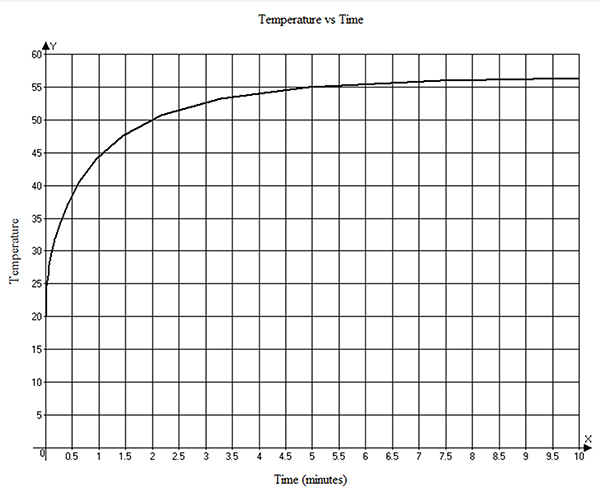
Figure 7. Temperature vs. time graph for the basic model.
Effect of board thickness. As the thickness of the dielectric increases, there is more board material for the heat to conduct through, so the temperature will presumably be lower with increased thickness. This is true to a point, but there reaches a point where increased thickness does not buy much. The typical PCB board is around 63 mils thick, and this is the thickness used for the basic model. But boards can be much thicker than that. FIGURE 8 illustrates the trace temperature as a function of board thickness. Note how the curve starts out fairly steep for thin boards, but then tends to stabilize as the board thickens.

Figure 8. Trace temperature decreases as the board gets thicker, up to a point.
The dynamics associated with this effect can be seen in the thermographs shown in FIGURES 9 and 10. These show the temperature of the board material at and below the trace. Imagine a surface cutting through the middle of the trace (at the 80mm point in the board) along the x-z plane. The view is toward the cross-section of the trace and shows the temperature gradient from the trace down toward the bottom of the board material. Figure 9 is for the 63 mil-thick board. Figure 10 is for the 240 mil board. There is not enough material in the thinner board for the heat to spread out much, but that is quite different for the thicker board. That is why the trace on the thicker board is significantly cooler.
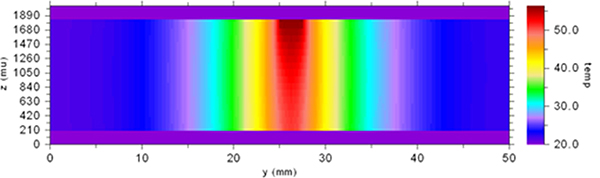
Figure 9. Vertical thermal profile of the 63 mils-thick board.
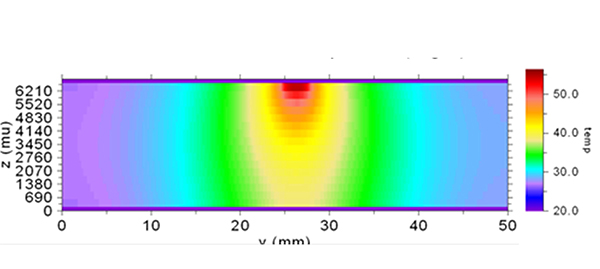
Figure 10. Vertical thermal profile of the 240 mil board.
Effect of resistivity. The resistivity of pure copper (at 20°C) is 1.68µΩ-cm. If the copper material on the board is plated (electrodeposited, or ED) copper, it will have a resistivity very close to this value.6 Rolled copper, on the other hand, probably originates as a copper alloy, and has a resistivity anywhere between 1.72 and 1.78µΩ-cm. Copper foil on PCBs can be either ED or rolled, but rolled is more common. The relationship between resistivity (ρ) of the material and the resistance (R) of the conductor is based on the geometry (area A and length L) of the conductor (Equation 1).
R = (ρ/A)*L [Eq. 1]
Recall the heating of the conductor is based on I2R power dissipation in the conductor. FIGURE 11 shows the relationship between the trace temperature and the resistivity of the copper. Our standard model assumed “pure” copper. So the temperature goes up as resistivity varies from that. Note the curve is linear, as would be expected.
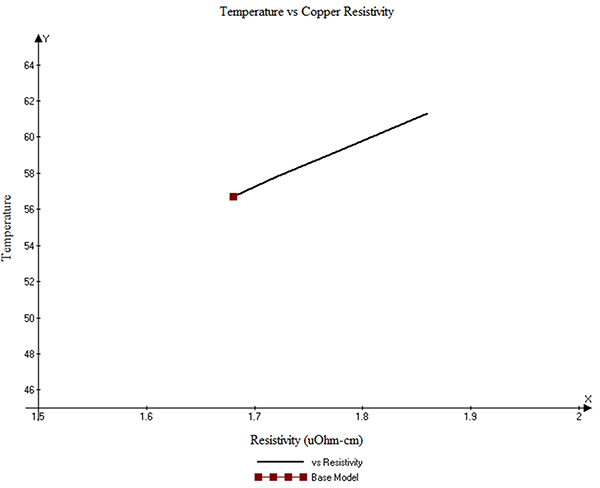
Figure 11. Trace temperature as a function of resistivity of the conductor.
Effect of HTC. As mentioned, HTC has components of convection and radiation. The authors have found in previous studies that for this temperature range, an HTC of 11 is fairly representative. An HTC of 6 would represent the situation of a trace in a vacuum (e.g., space). HTCs above 11 would represent some form of supplemental cooling, perhaps a heat sink or blowing air. We have looked at a range of HTCs from 6 (vacuum) to 18, but there is no practical way today to say what 18 actually means!7 FIGURE 12 is the relationship between trace temperature and HTC. The relationship shown in the figure is not surprising; as the convection cooling increases, the trace temperature goes down, sometimes dramatically.

Figure 12. Trace temperature as a function of HTC.
Effects of thermal conductivity coefficient. Start with the idea that the board material has the greatest impact on trace cooling. Then consider the idea that the thermal conductivity coefficient is the measure of how effective the board is at cooling the trace. Then recognize that this measure – thermal conductivity coefficient – is rarely provided in the datasheets of the material suppliers! And if it is provided, it frequently is provided as a single value, without specifying which coefficient it is. And if it is provided, it is often the value (through-plane) that is least important. This is an unfortunate state indeed.
FIGURE 13 shows the relationship between the thermal conductivity coefficient and the trace temperature. The in-plane (x-y, or horizontal) coefficient is clearly the one that has more effect on trace temperature.8
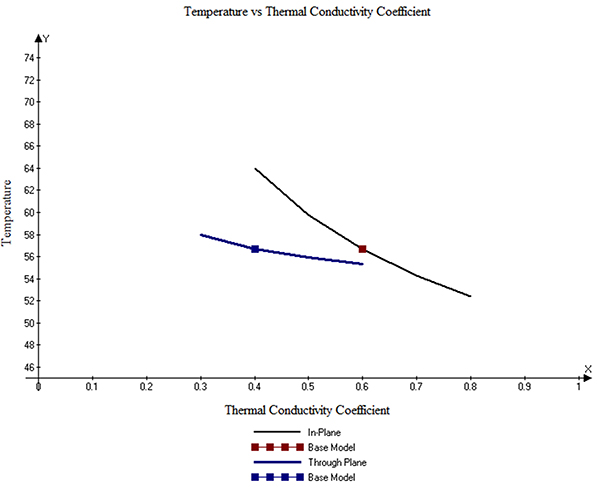
Figure 13. Trace temperature as a function of thermal conductivity coefficient.
Effect of trace thickness. Trace thickness is, of course, directly related to cross-sectional area. So a change in thickness will have a significant effect on the current/temperature relationship. But some might be surprised by how big an effect it can have. FIGURE 14 shows the relationship. The red dot in the figure shows the results of the basic model, using a 1.0 oz.-thick trace. The curve of temperature vs. thickness is moderately steep in this range. For this model, the sensitivity is about 1.0°C for a change of 0.003 mil thickness. This is likely the reason traces do not heat uniformly, as shown in Figure 4. Normal variations in trace thickness are well within this range.
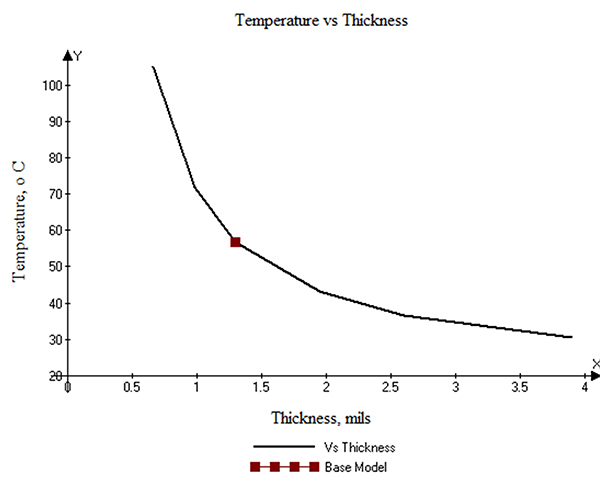
Figure 14. Trace temperature as a function of thickness.
Effect of planes. The results above are for a bare trace in isolation. Of course, on a typical board there will be many more adjacent traces that can have an impact on the trace temperature.9 But perhaps the largest external impact on trace temperatures can come from an adjacent plane. Many modern boards have internal planes, especially those with signal integrity issues. We performed one simulation with a 63 mils-thick board with two internal planes, one 20 mils under the trace, and the other 40 mils under the trace. These planes covered the entire surface area of that layer.
The impact of a plane is significant. It dropped the base temperature from 56.7° to 34.5°C. But more than that, it spread the heat (and temperature) out much more widely than was the case without the plane. FIGURE 15 shows the thermograph of the trace layer with the underlying planes. Compare this thermograph with that shown in Figure 6. There is a dramatic difference.
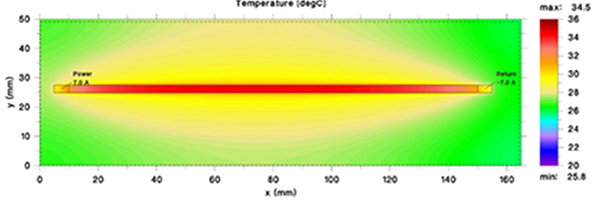
Figure 15. Impact of a plane on the thermal heat spreading.
The vertical distribution of the temperatures is also dramatically different. FIGURE 16 shows the vertical thermal profile for the case with the planes. Compare it with the case without a plane (Figure 9.)
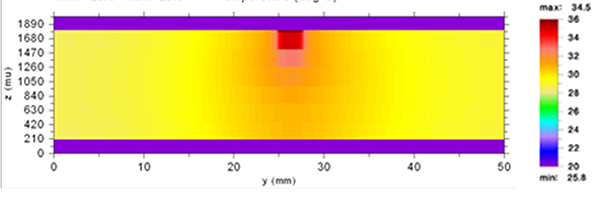
Figure 16. Vertical thermal profile with planes.
Conclusions
Many board designers need to work hard to optimize their designs. That often means designing the narrowest traces possible or that fabricators will permit. The reason is board area is expensive. Narrower traces mean more traces per layer, which mean fewer layers. And layers are expensive.
So if a trace is carrying a significant current, the designer wants to design the narrowest trace possible, consistent with achieving their temperature constraints. All the above suggests that can’t be achieved with charts, equations or formulas. Designers now need thermal simulation techniques to achieve their goals. There is a precedent for this. In the 1990s many designers began to worry about controlled impedance traces.10 At first we had equations we could use, but today those equations are not good enough. In the industry parlance, “field effect” solutions are required. Thermal simulation models, like TRM, employ the same quantitative techniques “field effect” solutions employ.
That is not to say there aren’t some general conclusions we can derive. For example, looking at Figure 11, a 10.7% increase in resistivity leads to an 8.1% increase in trace temperature. It may pay to look at the copper characteristics of the materials used by the material supplier and the board fabricator. Similarly, if the thermal conductivity coefficient can vary by, say, 0.3 between material choices, that may lead to a temperature reduction of as much as 10°C.11
Call to Action
What is apparent from the above analysis is additional research is necessary in two important areas. First, we do not know enough about how the HTC convection values change with temperature and conditions. A trace represents a small hot spot on an otherwise moderately uniform plane. We need to come up with ways to better estimate this effect.
Second, the industry needs to do a better job providing thermal conductivity information about the materials supplied. But further, the authors hypothesize that a) since the board material conducts heat in the in-plane direction more efficiently than it does in the through-plane direction, b) therefore, there should be a correlation between the ratio of resin to fiberglass and the trace temperature.
In addition, are there compounds that can be (economically) added to board materials (dielectrics) that can increase their thermal conductivity? For example, are there changes to the resin formulations that might accomplish this? Such approaches might improve the heat spreading capabilities of board materials almost to the point approximating the effects of underlying planes.
The authors don’t have the resources or contacts to conduct this kind of research. We hope others in the industry better equipped to do this type of research will do so.
Notes
1. Douglas Brooks, Ph.D. with Dr. Johannes Adam, PCB Trace and Via Currents and Temperatures: The Complete Analysis, 2006.
2. Thermal Risk Management (TRM). For more information on TRM and how to use it to construct thermal models, see http://www.adam-research.com. For detailed examples of how TRM can be used to simulate PCB traces, see reference 1, Chapter 6.
3. IPC-2152, “Standard for Determining Current Carrying Capacity in Printed Board Design,” August 2009. This is the most complete, most comprehensive, and best controlled study of trace heating and cooling effects ever undertaken in the industry.
4. For information on how thermal conductivity coefficients are measured, see Reference 1, Appendix 1.
5. For more information regarding the nonuniform heating of traces, see Reference 1, Chapter 12.
6. The authors discuss how to measure the resistivity of copper traces, and the difference between ED and rolled copper, in reference 1, Appendix 2.
7. Except it means that the trace is cooler!
8. For comparison, the thermal conductivity coefficient for copper is 385.
9. The authors perform a variety of such simulations in Chapter 6 of reference 1.
10. Controlled impedance traces are those designed to look like transmission lines, so those lines can be terminated in their characteristic impedance, thereby reducing signal reflections back on the traces.
11. This would apply for trace temperatures in the range of 50°C or so. For higher trace temperatures, the difference would be even greater.
Douglas Brooks, Ph.D., is owner of UltraCAD Design, a PCB design service bureau and author of PCB Currents: How They Flow, How They React; This email address is being protected from spambots. You need JavaScript enabled to view it.. Johannes Adam, Ph.D., CID, is founder of ADAM Research, a technical consultant for electronics companies, a software developer, and the author of the Thermal Risk Management simulation program.