Estimate the time constant of a process prior to conducting the DOE to prevent erroneous results.

When designing a DOE it is important to quantify the duration of the transient portion of the process before you begin. This parameter will evolve from the analysis as a time constant for the transient phase of the process. This parameter can then be used after starting the process to numerically define the appropriate time delay before starting the DOE. Knowing the magnitude of the time constant is also important in controlling the quality of the process. Without knowing the time constant, compensating adjustments are made during the transient portion of the process and the output of these will vary. The transient time is often a great deal larger than anticipated by conventional wisdom and can negatively impact the DOE outcome.

The two primary approaches used by fabrication engineers to resolve processing issues are either to employ their basic understanding of the process mechanism, or to use a DOE that is a statistical analysis method. In the case of a DOE, there are two basic assumptions. First, that all of the primary independent variables are included in the experiment, and second, that the process is not time dependent. If either of these underlying postulates are not the case, then the DOE will most likely be a failure.

In the past, most of us have experienced DOEs that generated results that were unrepeatable or erroneous. Given the pressures of the situation, we often resort to intuition to resolve technical problems. The purpose of this article is to analytically quantify one of the potential pitfalls mentioned above, which will corrupt the results of even the most carefully planned and executed DOE. In particular, many DOEs involve processes that, at least initially, are not stationary and a startup transient exists. Typical examples are wet chemistry processes. We all realize that initially such a process may be transient, and we may attempt to compensate for this by allowing the process to “settle down” before collecting any data. Often the marker that defines the “settling point” is something as significant as a subtle change in color.

Investigative Model

The process that will serve as the focus of interest for this analysis is the single chamber inline counter flow processor as shown in FIGURE 1. Processors of this design are used as etchers, developers, surface preparation, etc. This example is selected since it is one of the simplest wet chemistry processes in the industry.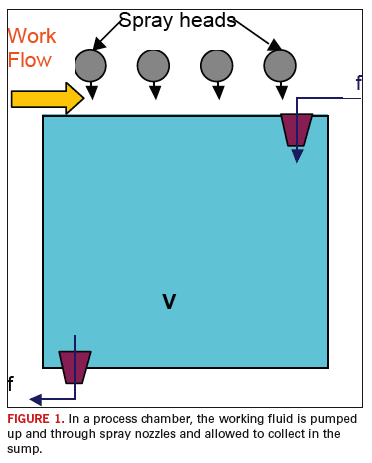



In this case, a working fluid is circulated at a rate, designated f, into and out of a holding tank. The fluid is pumped through the spray heads and onto the work piece (panel) where it removes the unwanted (and potentially troublesome) materials from the panel. The working fluid then drains from the panel and back into the holding tank bringing with it the unwanted superfluous material. This process increases the concentration of the superfluous material in the holding tank, consequently reducing the removal rate of this unwanted contaminate. It is assumed that the removal rate is inversely proportional to the concentration of the contaminate material. From this point forward we will draw on the analysis developed in the reference.

Analysis

One of the primary dependent variables characterizing the DOE would be the concentration of superfluous contaminate material introduced into the holding tank. That is, the ratio of the superfluous material to the volume of the tank, and it is a major variable influencing the dissolution rate of the working fluid. At any time ‘t’, the concentration ‘β’ is: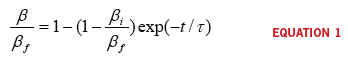



where:
β_ƒ    is the stationary concentration of the working fluid
β_i    is the initial concentration of the working fluid
    is the time constant of the transient portion of the process
t     is time

Analytical relationships for the solution concentration and the time constant in terms of the independent processing variables are found in the reference¹. We will first focus upon the time constant. The exponential behavior of such a process is depicted in FIGURE 2.



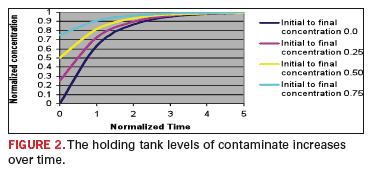
It is normally assumed that the process is stationary after four time constants (when the transient is 98% complete). Obviously, it is imperative that the time constant be determined.



where:
    is the turnover time of the holding tank and



where:
V     is the volume of holding tank
ρ    is the density of the superfluous material being removed from panel
A     is the active area over the holding tank
E_m     is the maximum removal rate of superfluous material from panel.

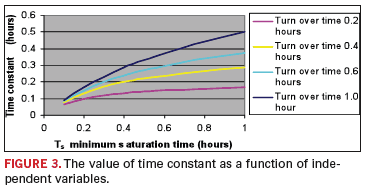
FIGURE 3 shows the value of the time constant as a function of these independent variables. It is not unreasonable to expect the time constant to range between 0.2 and 0.4 hours. The implication here is that the process does not become stationary until 0.8 to 1.6 hours (four time constants), and before starting the characterization of the stationary process (by a DOE), this much time should be allowed to elapse after startup or the validity of the evaluation will be in doubt.
Similar observations can be made concerning processing production grade product immediately after startup. For instance, since the concentration of superfluous material in the working fluid is increasing, the removal rate is decreasing, and consequently, the break point occurs later in the process.



This analysis has been carried out using a very simple process to illustrate the point. It is important that the physics of the process be understood before attempting to optimize it by carrying out a DOE. In particular, the time constant of the process should be estimated either by an analytical calculation or a series of measurements prior to conducting the classical DOE.   PCD&F

REFERENCE

1. “A Mathematical Model for an Inline Counter Flow Processor”, J. Lee Parker, Ph. D., IPC Apex, April 2008.

J. Lee Parker is president of JLP Consultants and can be reached at This email address is being protected from spambots. You need JavaScript enabled to view it..