Optimization routines save time by using automated methods to determine if performance goals are met.

Printed circuit board (PCB) design often begins with the development of signal integrity (SI) guidelines to ensure adequate performance of the final product. Most often the guidelines are based on traditional engineering practices through manual manipulation of circuit parameters and judicious interpretation of results. While such approaches do result in useful conclusions, they can also consume significant effort, only to reach sub-optimal conclusions. Alternatively, optimization routines can be used to aid in SI analysis and the development of PCB design guidelines.

Optimization routines have been well proven to aid analysis across a variety of common tasks, such as determining the optimal values for circuit parameters. In addition, there are several non-traditional applications where optimization can be useful, such as developing application-specific termination schemes.

With increasingly higher speeds and routing densities, proper signal integrity (SI) engineering is an important aspect of printed circuit board (PCB) design. At its basic levels, SI engineering involves the development of design guidelines for impedance control, termination, attenuation, and isolation. As design complexity increases, so does the associated SI analysis.

Where feasible, common industry practice (i.e., rules of thumb) can guide SI analysis on many issues with good results. In situations where more significant analysis is necessary, SI engineers can potentially benefit from non-traditional approaches. Optimization routines are engineering tools that are often useful in these situations, as they automate the process of tuning parametric values to achieve desired performance.

One of the more common applications of optimization routines is the development of equivalent-circuit models^1,2 of various passive interconnect. In these cases, the interconnect performance is measured in the lab in either time or frequency domains. Based on the measured performance and knowledge of the physical structure, a circuit topology is generated to approximate the performance. Optimization is then used to adjust the various circuit element values to best approximate the measured performance. In addition to model development, optimization routines are also commonly used for obtaining peak performance of completed links, such as determining optimal termination resistance.

Beyond these common applications, there are several non-traditional applications of optimization routines³ that can be of similar value. For example, it is often possible to use optimization routines to assist in developing unique circuit architectures or to optimize cost versus performance trade-offs.

Optimization Basics

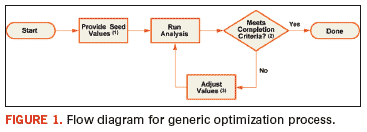
Optimization routines rely on an iterative process similar to that shown in Figure 1. For SI analysis, the process generally starts with a circuit model that has undesired simulated performance. Within the circuit model, a specific set of user-defined circuit parameters are selected, and these parameters are allowed to vary within a specified range. The parameters can be typical circuit values such as resistance and capacitance, or they can represent other physical quantities such as geometric length or dielectric constant. When the first simulation is run, these variable parameters are given user-defined seed values (Note 1 in Figure 1).

When the first simulation iteration is complete, the circuit performance is compared to the desired results using a set of user-defined metrics (Note 2 in Figure 1). The metrics can be simple, involving single-point values such as a specified voltage at a circuit node, or they can consist of complex functions such as relative match of two waveforms over time. If the simulated performance falls within a specified tolerance of the desired performance, then the optimization routine is complete and returns the original seed values.

If the simulated performance does not match the desired performance, then the internal optimization algorithm considers the previous results and calculates new values for the circuit’s variable parameters (Note 3 in Figure 1). Using the new values, the simulation is run again, the new simulated results are compared with the desired results, and the iterative process continues until the desired performance is obtained. The output of the process is the parametric values that allow the circuit performance to meet completion criteria.

The advantage in using optimization routines comes from the algorithm that calculates new values for the circuit’s variable parameters. Typically, these routines can adjust many variables simultaneously with fast convergence to an optimal operating point. Over the years, numerous algorithms have been developed^4-10, and each has its own respective strengths and weaknesses, the detailed discussion of which is beyond the scope of this article.

Challenge: Multi-Drop Bus

Optimization routines can be of significant help in many unexpected ways, one of which is aiding in the development of application-specific termination schemes. To provide an example of such an application, this section describes the process of using optimization routines to solve a common design challenge – the desire to increase effective memory depth without increasing pin count or routing density – accomplished by sharing address and data busses between multiple memory chips.

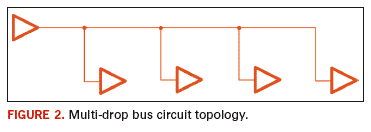
As shown in Figure 2, the associated net topology is called a multi-drop bus. Here, a single output buffer (often a processor ASIC) drives a trace with multiple stubs branching off the main trace with each stub having its own load device (memory chip). From an SI perspective, the challenges with this circuit topology include termination of each interconnect path, potential over-loading of the driver, and constructive/destructive interference from multiple reflections.

A common termination approach for such a topology is simply to terminate the far end of the primary signal path with a 50-Ohm termination resistor to VTT. While such a termination scheme works well for simple point-to-point circuit topologies, the signal waveforms shown in Figure 3 clearly demonstrate the undesired effects of inappropriately using this design practice in a situation that requires more analysis.

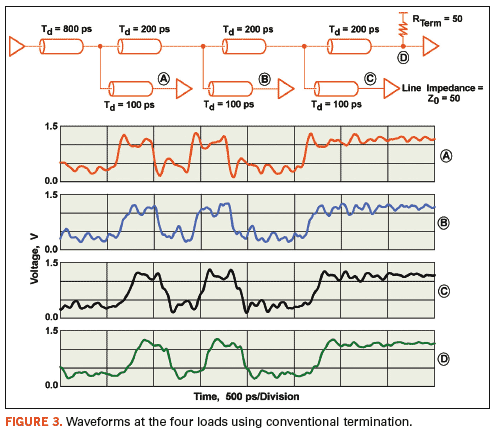
In this example based on 1.5-V HSTL signals, the signals collapse to levels within 90 mV of the 750-mV reference voltage, less than the 200-mV HSTL specification11 for AC conditions. Accordingly, the design needs to be changed for it to be reliably used in system applications. The difficulty here is in trying to determine what alternative circuit topologies to consider, and to then determine the appropriate values for each circuit element.

To obtain adequate SI performance in a multi-drop net such as this, there are numerous termination options whereby termination resistors are placed in shunt and/or series at various circuit nodes. However, the proper location and value of the termination resistors is not readily apparent, and it would take significant time and effort to manually explore all possible options.

Alternatively, we can use optimization routines to aid in determining proper termination architecture and associated resistor values. The process starts by tossing a veritable “kitchen sink” of termination options at the problem, as shown in Figure 4, where termination resistors are placed at each and every node, in both shunt and series configurations.

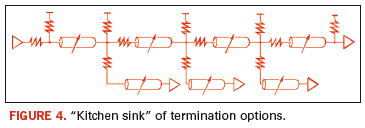
The process then uses optimization routines on the “kitchen sink” circuit, and the resulting parasitic values are inspected. If any parasitic value falls outside a useful range, the entire element is removed from the circuit, and optimization is performed again. The process continues until all parasitic values approach reasonable and practical values and the resulting signal integrity is adequate.

One common feature most optimization routines share is a decreased efficiency with an increase in the number of variables. If all twelve resistors and all seven line impedances in the above example were allowed to vary independently, the optimization process would take considerable time and the results could be impractical to implement. Alternatively, it is reasonable to constrain the primary path from the driver to the last receiver to one common line impedance, while all the stubs rely on different impedances. Similarly, the three resistors at each transmission line split can be chosen to be the same value as those on the other splits, thus further reducing the number of variables.

With most optimization routines, seed and limit values are needed. For the transmission lines, a 50-Ohm impedance is most-often used and will be the suggested nominal value for the simulations. For the limits, practical values are chosen to range from 25 Ohm to 100 Ohm. For the shunt resistors, nominal 50 Ohm values are chosen with limits of 1 Ohm and 1,000 Ohm. For the series resistors, 10 Ohm nominal, 1 Ohm minimum, and 1000 Ohm maximum values are chosen. For all resistors, values approaching 1 Ohm will be considered shorts and values approach 1,000 Ohm will be considered opens. In all, the nineteen possible variables are reduced to eight.

Using the circuit topology of Figure 4 and the parametric values discussed above, optimization is performed with a goal of maximizing the eye opening at all four loads. The results of the first optimization step indicates that the circuit performed best when the source-series resistor at the driver was 1 Ohm, which is at the bottom limit. In addition, the intermediate series terminators along the primary transmission path provide best performance when they have low values. Accordingly, we can effectively remove these circuit elements by replacing them with direct shorts. Similarly, the shunt resistor values at the driver and along the primary signal path are sufficiently high that we consider them to be opens, and thus remove them from the circuit. The resulting circuit is shown in Figure 5, which is now much more practical to implement.

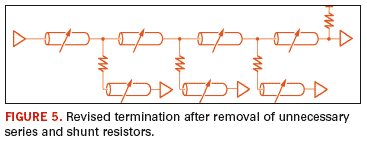
Using the revised circuit, optimization is performed again to fine-tune the remaining parasitic values. We then round off the results to practical values, and the resulting circuit performance is shown in Figure 6.

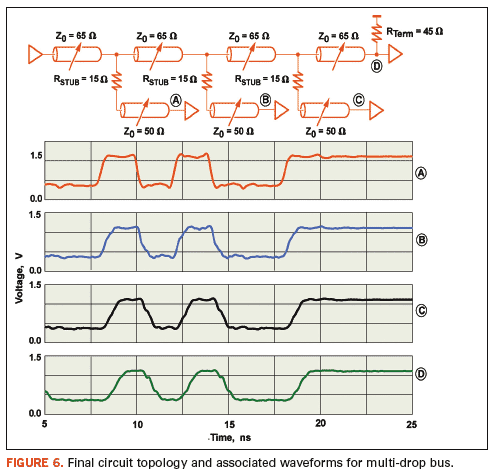
The original non-optimized circuit produced poor signal waveforms with an eye opening of just 90 mV beyond the reference voltage and failed to meet the HSTL specification. Through the demonstrated iterative optimization process, the eye opening improved to over 300 mV, the signal quality improved dramatically, and the signals now exceed the HSTL specification by 100 mV.

In addition to determining reasonable parasitic values for the termination resistors, optimization routines also aided in the development of the application-specific termination architecture. Where it could have taken hundreds or even thousands of simulations and many weeks of hands-on time using traditional manual approaches to produce the same results, the use of optimization routines in this case reduced the number of manual steps down to three and reduced the hands-on effort to a few hours.

Conclusions

Judicious use of optimization routines can save significant effort using automated methods to determine appropriate values to meet specific user-defined performance goals, subject to constraints. In addition, optimization can be of tremendous help in determining appropriate circuit topologies for both models and circuits, and can often be used to navigate through the various conflicting goals of cost, reliability, and performance.

Optimization should be used with caution, because issues such as non-convergence and inappropriate results can occur. Therefore, it is imperative that all results are validated, and it is recommended that users familiarize themselves with all optimization options prior to using this procedure. PCD&F

REFERENCES

1. Nimmagadda, S., A. Moncayo, and J. Dillon. Measurement, Modeling and Simulation of a High Speed Digital System Using VNA and HSPICE. Northcon. 1996. Seattle, WA: IEEE.
2. Huang, C.-C., et al. Extraction of accurate package models from VNA measurements. in Electronics Manufacturing Technology Symposium. 2000. Santa Clara, CA: IEEE.
3. Zabinski, P., B. Buhrow, B. Gilbert, and E. Daniel, Application of Optimization Routines in Signal Integrity Analysis, DesignCon 2007, Santa Clara, CA, January 29 to February 1, 2007.
4. Yun, I. and G.S. May. Passive Circuit Model Parameter Extraction Using Genetic Algorithms. in 1999 Electronic Components and Technology Conference. 1999. San Diego, CA: IEEE.
5. Levenberg-Marquardt Algorith, http://en.wikipedia.org/wiki/Levenberg-Marquardt_algorithm
6. Ananth Ranganathan, The Levenberg-Marquardt Algorithm, cc.gatech.edu/people/home/ananth/docs/lmtut.pdf, June 2004.
7. Fletcher, R., Practical Methods of Optimization, NY, Wiley, 1993.
8. Gill, P.E., Murray, W. and Wright, M.H., Practical Optimization, Academic Press, London, 1981.
9. Levenberg, K. ”A method for the solution of certain problems in least squares,” Quart. Appl. Math., 2, 164-168, 1944.
10. Marquardt, D. ”An algorithm for least-squares estimation of nonlinear parameters,” SIAM J. Appl. Math., 11, 431-441, 1963.
11. High Speed Transceiver Logic (HSTL): A 1.5 V Output Buffer Supply Voltage Based Interface Standard for Digital Integrated Circuits. 1995, Electronic Industries Association.
12. 72Mb M-die DDRII SRAM Specification, 2006, Samsung.

Pat Zabinski is a principal engineer, Ben Buhrow is a senior engineer, Barry K. Gilbert is director of the special-purpose processor development group and Erik S. Daniel is deputy director of the special-purpose processor development group, all at the Mayo Clinic; This email address is being protected from spambots. You need JavaScript enabled to view it..